Язык науки стремительно меняется в современном мире. История развития физики насчитывает уже не одно столетие. За это время изучено огромное количество разнообразных явлений природы, открыты фундаментальные законы физики, объясняющие различные экспериментальные факты. Каждый раз, сталкиваясь с новыми природными объектами, ученые вводят в язык науки новые категории, термины и понятия.
До недавнего времени геометрические модели различных природных конструкций традиционно строились на основе сравнительно простых геометрических фигур: прямых, многоугольников, окружностей, многогранников, сфер. Однако очевидно, что этот классический набор, вполне достаточный для описания элементарных структур, становится плохо применимым для характеристики таких сложных объектов, как очертание береговых линий материков, поле скоростей в турбулентном потоке жидкости, разряд молнии в воздухе, пористые материалы, форма облаков, снежинки, пламя костра, контуры дерева, кровеносно-сосудистая система человека, поверхность клеточной мембраны и др. В последние 15-20 лет для описания этих и им подобных образований ученые все чаще используют новые геометрические понятия. Одним из таких понятий, изменившим многие традиционные представления о геометрии, явилось понятие фрактала. Оно было введено в обращение замечательным французским математиком польского происхождения Бенуа Мандельбротом в 1975 году. И хотя в математике похожие конструкции в той или иной форме появились уже много десятков лет назад, в физике ценность подобных идей была осознана лишь в 70-е годы нашего столетия.
Основой новой геометрии является идея самоподобия. Она выражает собой тот факт, что иерархический принцип организации фрактальных структур не претерпевает значительных изменений при рассмотрении их через микроскоп с различным увеличением. В результате эти структуры на малых масштабах выглядят в среднем так же, как и на больших. Здесь следует провести разницу между геометрией Евклида, имеющей дело исключительно с гладкими кривыми, и бесконечно изрезанными самоподобными фрактальными кривыми. Элементы кривых у Евклида всегда самоподобны, но тривиальным образом: все кривые являются локально прямыми, а прямая всегда самоподобна. Фрактальная же кривая, в идеале, на любых, даже самых маленьких масштабах не сводится к прямой и является в общем случае геометрически нерегулярной, хаотичной. Для нее, в частности, не существует и понятия касательной в точке, так как функции, описывающие эти кривые, являются в общем случае недифференцируемыми.
Возможно, что наиболее убедительным аргументом в пользу изучения фракталов является их бросающаяся в глаза красота.
Многие крупные достижения науки о фракталах стали возможны только с использованием методов вычислительной математики, которая в настоящее время немыслима без применения современных компьютеров. "Компьютерные эксперименты" позволили получить достаточно полное представление о разнообразных фрактальных структурах и причинах их возникновения. Часто теоретическое моделирование этих структур подчас даже опережало экспериментальные методы изучения реальных природных объектов сложной формы.
В настоящее время при помощи сравнительно простых алгоритмов появилась возможность создавать трехмерные изображения фантастических ландшафтов и форм, которые способны преобразовываться во времени в еще более захватывающие картины. С другой стороны, часто искусственные изображения фракталов столь схожи с естественными, природными формами, что их невозможно отличить друг от друга.
История фракталов
История фрактальной геометрии тесно связана с именами таких известных математиков, как Вейерштрасс, Кантор, Пеано, Хаусдорф, Безикович, Кох, Серпинский и др. Так Вейерштрасс впервые ввел в обращение непрерывную, но нигде не дифференцируемую функцию. Хаусдорф в 1919 г. ввел понятие о дробной размерности множеств и привел первые примеры таких множеств. Среди них были канторовское множество, кривая Коха и другие экзотические объекты, мало в то время известные за пределами чистой математики.
Большой вклад в будущую фрактальную геометрию внесли также знаменитые работы французских математиков Г. Жулиа и П. Фату, которые в начале 20 века занимались теорией рациональных отображений в комплексной плоскости. Практически полностью забытая, их деятельность получила неожиданное развитие в начале восьмидесятых годов, когда с помощью компьютеров математикам удалось получить прекрасные картины, показывающие примеры таких отображений. Это уже была эра фрактальной геометрии, поскольку незадолго до этого, в середине 70-х годов, в науке появился совершенно новый термин "фрактал", характеризующий нерегулярный, но самоподобный объект, который удобно было характеризовать нецелочисленной размерностью.
Заслуживает внимания тот факт, что появление фракталов (еще не получивших этого имени) в математической литературе около ста лет назад было встречено с прискорбной неприязнью, как это бывало и в истории развития многих других математических идей. Общее мнение признало их патологией, представляющей интерес только для исследователей, злоупотребляющих математическими причудами, а не для настоящих ученых.
В результате усилий Бенуа Мандельброта такое отношение изменилось, и фрактальная геометрия стала уважаемой прикладной наукой. Мандельброт ввел в употребление термин фрактал, основываясь на теории фрактальной (дробной) размерности Хаусдорфа, предложенной в 1919 году. За много лет до появления его первой книги по фрактальной геометрии, Мандельброт приступил к исследованию появления монстров и других патологий в природе. Он отыскал нишу для имевших дурную репутацию множеств Кантора, кривых Пеано, функций Вейерштрасса и их многочисленных разновидностей, которые считались нонсенсом. Он и его ученики открыли много новых фракталов, например, фрактальное броуновское движение для моделирования лесного и горного ландшафтов, флуктуации уровня рек и биения сердца.
Траектории частиц броуновского движения, которым занимались Роберт Броун еще в 1828 году и Альберт Эйнштейн в 1905 году, представляют собой пример фрактальных кривых, хотя их математическое описание было дано только в 1923 году Норбертом Винером.
Различные древовидные фракталы применялись не только для моделирования деревьев-ростений, но и бронхиального дерева (воздухоносные ветви в легких), работы почек, кровеносной системы и др. Интересно отметить предположение Леонардо да Винчи о том, что все ветки дерева на данной высоте, сложенные вместе, равны по толщине стволу (ниже их уровня). Отсюда следует фрактальная модель для кроны дерева в виде поверхности-фрактала.
Примеры различных фрактальных структур можно встретить во многих явлениях природы. Фрактальные образы с успехом используются при описании хаотического поведения нелинейных динамических и диссипативных систем, неоднородного распределения материи во Вселенной, при исследовании трещин и дислокационных скоплений в твердых телах, при изучении электрического пробоя, диффузии и агрегации частиц, роста кристаллов и т. д.
Язык фрактальной геометрии необходим, например, при изучении поглощения или рассеяния излучения в пористых средах, для характеристики сильно развитой турбулентности, при моделировании свойств поверхности твердых тел, для описания молнии, при анализе процессов усталостного разрушения материалов, при исследовании различных стадий роста вещества за счет диффузии и последующей агрегации, в квантовой механике при описании геометрической структуры волновых функций в точке перехода Андерсона металл-диэлектрик. Удивительно то, что сходные геометрические формы встречаются в совершенно различных областях науки: в астрофизике при описании процессов кластеризации галактик во Вселенной, в картографии при изучении форм береговых линий и разветвленной сети речных русел и, например, в биологии, при анализе строения кровеносной системы или рассмотрении сложных поверхностей клеточных мембран.
Для чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации.
· Геометрические фракталы
· Алгебраические фракталы
· Стохастические фракталы
Рассмотрим эти различные виды фракталов более подробно.
Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.
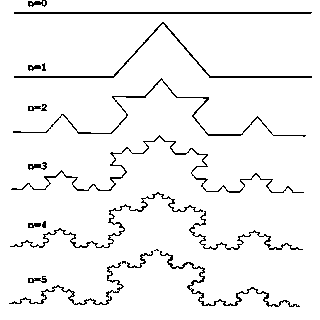
Рис 1. Построение триадной кривой Кох.
Рассмотрим один из таких фрактальных объектов - триадную кривую Кох. Построение кривой начинается с отрезка единичной длины (рис.1) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис.1 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным обьектом.
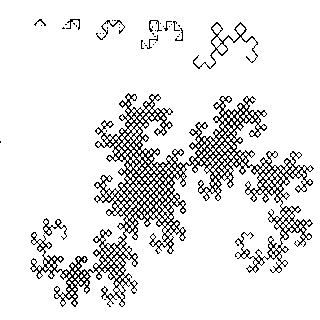
Рис 2. Построение "дракона" Хартера-Хейтуэя.
Для получения другого фрактального объекта нужно изменить правила построения. Пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на этот образующий элемент так, чтобы угол был сверху. Можно сказать, что при такой замене происходит смещение середины звена. При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться. На рис.2 представлены несколько первых поколений и 11-е поколение кривой, построенной по вышеописанному принципу. Предельная фрактальная кривая (при n стремящемся к бесконечности) называется драконом Хартера-Хейтуэя.
В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов, береговой линии. Двухмерные геометрические фракталы используются для создания объемных текстур (рисунка на поверхности обьекта).
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.
Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.
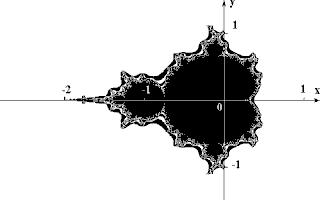
Рис 3. Множество Мандельброта.
В качестве примера рассмотрим множество Мандельброта (см. pис.3 и рис.4). Алгоритм его построения достаточно прост и основан на простом итеративном выражении:
Z[i+1] = Z[i] * Z[i] + C,
где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки C прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это означает, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например 200-500) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки C (если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).
Рис 4. Участок границы множества Мандельброта, увеличенный в 200 pаз.
Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки имеющие черный цвет). Точки принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).
Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Существуют и другие классификации фракталов, например деление фракталов на детерминированные (алгебраические и геометрические) и недетерминированные (стохастические).
Фракталами называются геометрические объекты: линии, поверхности, пространственные тела, имеющие сильно изрезанную форму и обладающие свойством самоподобия. Слово фрактал произошло от латинского слова fractus и переводится как дробный, ломаный. Самоподобие как основная характеристика фрактала означает, что он более или менее единообразно устроен в широком диапазоне масштабов. Так, при увеличении маленькие фрагменты фрактала получаются очень похожими на большие. В идеальном случае такое самоподобие приводит к тому, что фрактальный объект оказывается инвариантным относительно растяжений, т. е. ему, как говорят, присуща дилатационная симметрия. Она предполагает неизменность основных геометрических особенностей фрактала при изменении масштаба.
Конечно, для реального природного фрактала существует некоторый минимальный масштаб длины 
, такой, что на расстояниях 
его основное свойство — самоподобие — пропадает. Кроме того, на достаточно больших масштабах длин 
, где 
— характерный геометрический размер объектов, это свойство самоподобия также нарушается. Поэтому свойства природных фракталов рассматриваются лишь на масштабах l, удовлетворяющих соотношению 
– Такие ограничения являются довольно естественными, потому что, когда мы приводим в качестве примера фрактала — изломанную, негладкую траекторию броуновской частицы, то мы понимаем, что этот образ является очевидной идеализацией. Дело в том, что на маленьких масштабах сказывается конечность массы и размеров броуновской частицы, а также конечность времени соударения. При учете этих обстоятельств траектория броуновской частицы становится плавной кривой.
Регулярный фрактал, называемый салфеткой Серпинского, получается последовательным вырезанием центральных равносторонних треугольников так, как показано на рис. 5.
рис. 5 Построение салфетки Сегпинского.
В результате получается "дырявая" фигура (см. рис. 5), состоящая из бесконечного числа изолированных точек. Фрактальная размерность салфетки Серпинского подсчитывается по формуле
(1.1)
Здесь на нулевом шаге мы имеем один равносторонний треугольник с длиной стороны l = 1, а на следующем — три равносторонних треугольника со сторонами l' = 1/2. Поэтому l = 1, N(1) = 1, а l' = 1/2, N(lf) = 3. Салфетка имеет нулевую площадь, поскольку нетрудно проверить, что в процессе ее построения была исключена площадь, в точности равная площади исходного треугольника. Об этом же говорит и значение фрактальной размерности D < 2, которая меньше размерности плоскости, на которой находится этот объект.
Подсчитаем теперь периметр исключенных областей. Если сторона исходного треугольника была равна 1, то на первом шаге построения периметр центрального треугольника равен 3/2. На втором шаге к нему добавляются три новых треугольника с общим периметром, равным 9/4 и т.д. Очевидно, что на п-м шаге периметр
определяется
рис. 6. Салфетка Серпинского.
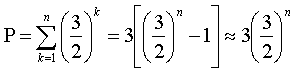(1.2)
Поэтому формула для периметра, выраженного через этот масштаб, приобретает вид, схожий с формулой для длины береговой линии
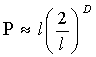(1.3)
где D определяется формулой (1.1).
Word документ "Теория фракталов"-210 Kb |
