или квадратичные:
Метод "Систем Итерируемых Функций" (Iterated Functions System - IFS) появился в середине 80-х годов как простое средство получения фрактальных структур.
IFS представляет собой систему функций из некоторого фиксированного класса функций, отображающих одно многомерное множество на другое. Наиболее простая IFS состоит из аффинных преобразований плоскости:
X' = A*X + B*Y + C
Y' = D*X + E*Y + F
Аффинное преобразование - композиция линейного преобразования и параллельного переноса. В двумерном пространстве для полного представления аффинного преобразования достаточно задать 6 коэффициентов.
В 1988 году известные американские специалисты в теории динамических систем и эргодической теории Барнсли и Слоан предложили некоторые идеи, основанные на соображениях теории динамических систем, для сжатия и хранения графической информации. Они назвали свой метод методом фрактального сжатия информации. Происхождение названия связано с тем, что геометрические образы, возникающие в этом методе, обычно имеют фрактальную природу в смысле Мандельброта.
На основании этих идей Барнсли и Слоан создали алгоритм, который, по их утверждению, позволит сжимать информацию в 500-1000 раз. Вкратце метод можно описать следующим образом. Изображение кодируется несколькими простыми преобразованиями (в нашем случае аффинными), т.е. коэффициентами этих преобразований (в нашем случае A,B,C,D,E,F).
Например, закодировав какое-то изображение двумя аффинными преобразованиями, мы однозначно определяем его с помощью 12-ти коэффициентов. Если теперь задаться какой-либо начальной точкой (например X=0 Y=0) и запустить итерационный процесс, то мы после первой итерации получим две точки, после второй - четыре, после третьей - восемь и т.д. Через несколько десятков итераций совокупность полученных точек будет описывать закодированное изображение. Но проблема состоит в том, что очень трудно найти коэффициенты IFS, которая кодировала бы произвольное изображение.
Для построения IFS применяют кроме аффинных и другие классы простых геометрических преобразований, которые задаются небольшим числом параметров. Например, проективные:
X' = (A1*X + B1*Y + C1) / (D1*X + E1*Y + F1)
Y' = (A2*X + B2*Y + C2) / (D2*X + E2*Y + F2)
X' = A1*X*X + B1*X*Y + C1*Y*Y + D1*X + E1*Y + F1
Y' = A2*X*X + B2*X*Y + C2*Y*Y + D2*X + E2*Y + F2
преобразования на плоскости.
В качестве примера использования IFS для построения фрактальных структур, рассмотрим кривую Коха (Рис.1) и "дракона" Хартера-Хейтуэя (Рис.2). Выделим в этих структурах подобные части и, для каждой из них вычислим коэффициенты аффинного преобразования. В аффинный коллаж будет включено столько аффинных преобразований, сколько существует частей подобных целому изображению.
Рис 7. Заготовка для построения IFS "дракона" Хартера-Хейтуэя.
Построим IFS для "дракона" Хартера-Хейтуэя. Для этого расположим первое поколение этого фрактала на сетке координат дисплея 640 x 350 (Рис.7). Обозначим точки получившейся ломаной A, B, C. По правилам построения, у этого фрактала две части, подобные целому - на рис.5 это ломаные ADB и BEC. Зная координаты концов этих отрезков, можно вычислить коэффициенты двух аффинных преобразований, переводящих ломаную ABC в ADB и BEC:
X' = -0.5*X -0.5*Y + 490
Y' = 0.5*X -0.5*Y + 120
X' = 0.5*X -0.5*Y + 340
Y' = 0.5*X +0.5*Y - 110
Задавшись начальной стартовой точкой (например X=0 Y=0) и итерационно действуя на нее этой IFS, после десятой итерации на экране получим фрактальную структуру, изображенную на рис.8, которая представляет собой "дракон" Хартера-Хейтуэя. Его кодом (сжатым описанием) является набор коэффициентов двух аффинных преобразований.
Рис 8. "Дракон" Хартера-Хейтуэя, постpоенный с помощью IFS в пpямоугольнике 640x350.
Аналогично можно построить IFS для кривой Кох. Нетрудно видеть, что эта кривая имеет четыре части, подобные целой кривой. Для нахождения IFS опять расположим первое поколение этого фрактала на сетке координат дисплея 640 x 350 (Рис.9).
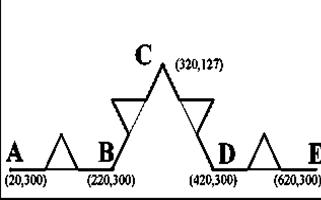
Рис 9. Заготовка для построения IFS кpивой Кох.
Для ее построения требуется набор аффинных преобразований, состоящий из четырех преобразований:
| X' = 0.333*X + 13.333 |
Результат применения этого аффинного коллажа после десятой итерации можно увидеть на рис.10.
Рис 10. Кpивая Кох, постpоенная с помощью IFS в пpямоугольнике 640x350.
Использование IFS для сжатия обычных изображений (например фотографий) основано на выявлении локального самоподобия, в отличие от фракталов, где наблюдается глобальное самоподобие и нахождение IFS не слишком сложно (мы сами только-что в этом убедились). По алгоритму Барнсли происходит выделение в изображении пар областей, меньшая из которых подобна большей, и сохранение нескольких коэффициентов, кодирующих преобразование, переводящее большую область в меньшую. Требуется, чтобы множество "меньших" областей покрывало все изображение. При этом в файл, кодирующий изображения будут записаны не только коэффициенты, характеризующие найденные преобразования, но и местоположение и линейные размеры "больших" областей, которые вместе с коэффициентами будут описывать локальное самоподобие кодируемого изображения. Восстанавливающий алгоритм, в этом случае, должен применять каждое преобразование не ко всему множеству точек, получившихся на предыдущем шаге алгоритма, а к некоторому их подмножеству, принадлежащему области, соответствующей применяемому преобразованию.
Пример систем итерируемых функций
Одним из наиболее ярких примеров среди различных систем итерируемых функций, несомненно, является открытая М. Барнсли система из четырех сжимающих аффинных преобразований, аттрактором для которой является множество точек, поразительно напоминающее по форме изображение листа папоротника. Ее можно представить в виде следующей таблицы
| a |
b |
c |
d |
e |
f |
p |
| 0 |
0 |
0 |
0.16 |
0 |
0 |
0.01 |
| 0.85 |
0.04 |
-0.04 |
0.85 |
0 |
1.6 |
0.85 |
| 0.2 |
-0.26 |
0.23 |
0.22 |
0 |
1.6 |
0.07 |
| -0.15 |
0.28 |
0.26 |
0.24 |
0 |
0.44 |
0.07 |
Каждая строчка этой таблицы соответствует одному аффинному преобразованию с коэффициентами а, b, с, d, е, f в соответствии с выражением
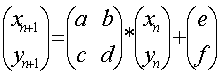
В последнем столбце таблицы приведены вероятности р, в соответствии с которыми в методе случайных итераций выбирается то или иное преобразование.
Результат действия этой системы функций на некоторую начальную точку для разного числа итераций приведен на рис. 1.43. Видно, как с ростом числа итераций действительно
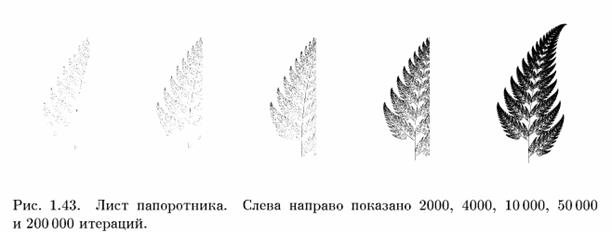
возникает все более и более четкое изображение листа папоротника, удивительным образом напоминающее существующее в природе растение.
Это множество точек бесконечно самоподобно, как и полагается всякому фракталу. Как следует из рис. 11, увеличенные малые фрагменты изображения подобны целому. Для разрешения этих фрагментов необходимо только, чтобы число итераций было достаточно велико.
Таким образом, чем больше используемое разрешение, тем больше точек требуется внести в память компьютера для того, чтобы построить соответствующее изображение. С другой стороны, запоминать координаты этих точек вовсе не требуется, так как они каждый раз могут быть заново получены с использованием системы функций, заданных таблицей
Рис. 11. Увеличенный фрагмент листа папоротника
В результате всего 28 чисел содержат всю необходимую информацию об этом нетривиальном рисунке! Возникает мысль, а нельзя ли подобным образом "кодировать" и другие изображения. Эта идея, будучи реализованной на практике, позволила бы сжимать изображения в десятки или даже в сотни раз. И действительно в 1988 г. она была успешно воплощена Барнсли и Слоаном в созданной ими совместно компании по кодированию и сжатию графической информации с помощью соответствующим образом подобранной системы функций.
Для генерации фрактальных рисунков можно написать алгоритм программы в Паскале, Бейсике или в других языках программирования. Есть множество литературы в которой подробно рассмотрено написание алгоритма программы для генерации фракталов, например, Р. М. Кроновер «Фракталы и хаос в динамических системах. Основы теории», в содержании рассмотрено теория о фракталах а так же примеры с написанием программ для генерации фракталов. Но на сегодняшний день существует большое количество уже написанных программ генерации фрактальных рисунков. Рассмотрим одну из них- Fractal Explorer версии 2.02.
При запуске Fractal Explorer появляется пустое окошко, сверху находится панель инструментов.
Слева которой активны шесть иконок. Первые пять для генерации новых, а шестое для открытия ранее сохраненного. Например, при нажатии на первою иконку 
начинает генерироваться фрактал Мандельброта, причем генерация происходит в реальном времени. В меню Size можно поменять разрешение для фрактальной картинки. По умолчанию 300 х 300, из предоставленного списка разрешений можно либо прибавить, либо убавить. При увеличении разрешения фрактал уже генерируется дольше чем раньше, так как компьютеру становится сложнее рассчитать фрактал на большее количество точек. При двойном клике левой клавиши мыши фрактал увеличивается, но не просто он становится крупнее, а просчитывается заново. После того как фрактал сгенерировался, можно изменить некторые параметры генерации фрактала. При нажатии 
появляется окошко,
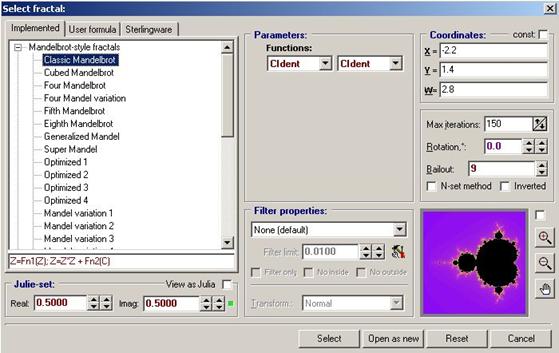
в котором можно изменить итерационную формулу, количество итераций, параметры функций, и множество других настроек.
Так же можно построить систему итерируемых функций, фракталом которой является лист папоротника. По умолчанию для построения этого фрактала стоит 100 итераций. И если лист папоротника начать увеличивать, то при сравнительно небольшом увеличении видно, что он состоит из точек. При изменении 100 итераций на 5000, увеличенный часть листка папоротника уже состоит из множества листочков папоротника.
В заключении описании программы Fractal Explorer, можно сказать, что очень интересно наблюдать затем как рисуется фрактал, какой палитрой он раскрашивается. Сильно понравившийся фрактал, можно сохранить или напечатать.
Может быть, в будущем новые идеи фрактальной геометрии помогут нам изучить многие загадочные явления окружающей природы.
В настоящее время фракталы и мультифракталы стремительно вторгаются во многие области физики. Фрактальные методы обработки изображений и распознавания образов, использующие новые понятия, дают возможность исследователям применить этот математический аппарат для количественного описания огромного количества природных объектов и структур.
Word документ "Теория фракталов"- 210 Kb |
